【オセロ】ビットボードで石を置ける場所を計算して、ビットボードの凄さに触れよう

先日こんな記事を書いたのですが、よく考えたらあんまりちゃんと中身まで解説できてなかったなと思ったのと、もっといい方法を思いついたのでもっと単純化して説明します。

前提: ビットボードとは？

ビットボードが何か分かっている方は次の節まで飛ばしていただいて構いません。

プログラム上で以下のオセロの盤面を表そうと思ったとき、どのようにすべきでしょうか？

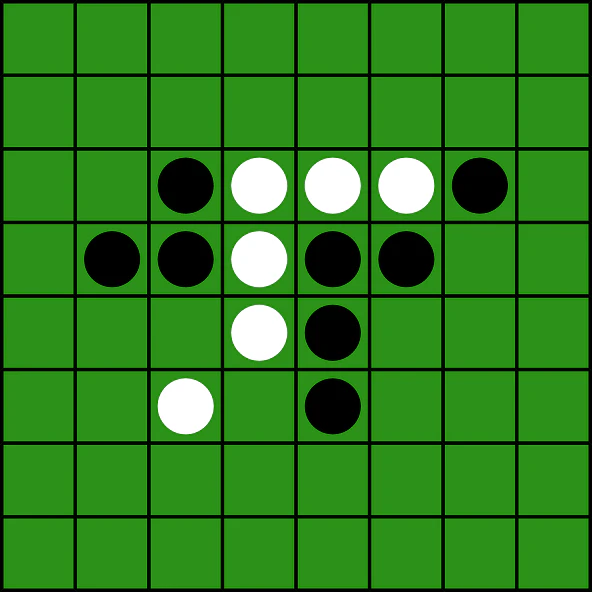
パッと思いつくのは、二次元配列でしょうか。

board_othello = [
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "B", "W", "W", "W", "B", "-"],
    ["-", "B", "B", "W", "B", "B", "-", "-"],
    ["-", "-", "-", "W", "B", "-", "-", "-"],
    ["-", "-", "W", "-", "B", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"]
]

ビットボードの場合、こうなります。

black = 0x226c08080000
white = 0x1c1010200000

一見すると何をやっているのかわかりませんが、これはオセロのボードを64bit整数に見立てています。ボードの各マスは空きマス/黒/白の3つの状態を取るので、黒と白の石を別々の64bit整数で表すことによって表現しています。

2進数にして、8×8に並べ替えてみるとなんとなく分かると思います。

ビットの並び順は以下の画像のようになっています。

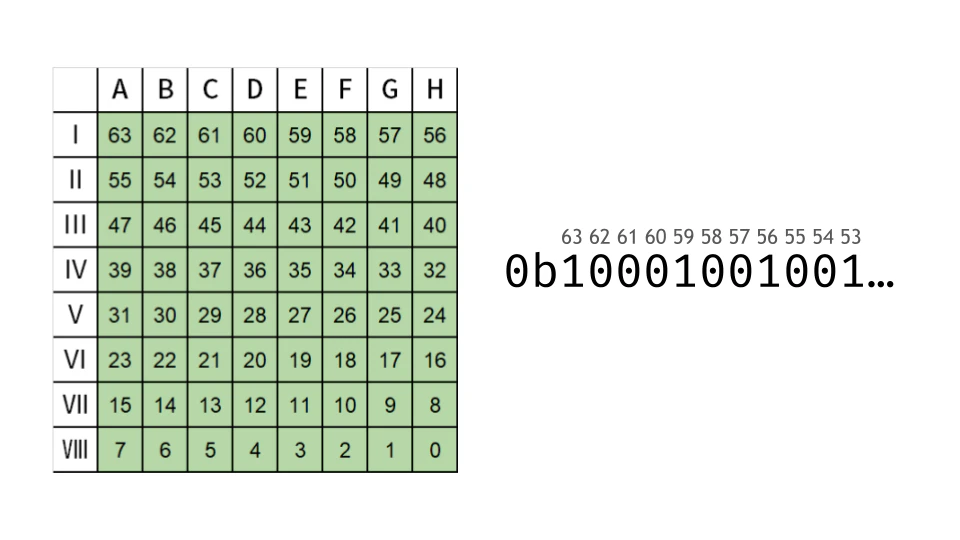
ビットボードは計算が高速、メモリ使用量が少ない(ただの64bitの数字なので)などのメリットがありますが、その分何をやっているのか分かりづらくなってしまいます。

せっかくなので、ビットボードがどう動いているのか完全理解してみましょう。以下にビットボードでオセロの合法手(石を置ける位置)を計算する手順を示します。

できるだけ単純化する

8×8=64マスで考えると複雑すぎるので、2×4=8マスで考えます。現在は黒の手番です。

もはやオセロと呼べるかどうか怪しいですが、ひとまずここから黒の石を置ける場所を探していきます。

説明の簡略化のため、ここでは右側だけ調べることにします。

隣が相手の石かどうか確認する

まず、自分の石を全部1個ずらします。移動前の石を半透明にして示しています。

おや、自分の石と相手の石が同じマスにありますね。

当たり前ではありますが、自分の石の隣にある相手の石はひっくり返せるかもしれない石です。

別のボードを用意して、重なった部分をマークしておきましょう。

ひっくり返せない石のマークを消す

さて、ボードの一番右にある相手の石にもマークをつけてしまいましたが、よく考えたらこれ以上右は盤外なので、この石はひっくり返せませんね。

これは右だけでなく、ボードの端はどちらもひっくり返せないことになります。というわけで、残念ですがさっきつけたマークのうちボードの両端にあるものには消えてもらうことにしましょう。

これで、『ひっくり返せるかもしれない相手の石』の位置がマークとして残りました。

さらに隣を確認する

このボードの幅は4マスです。2つの石で相手の石を挟むので、最大で2個相手の石をひっくり返せる可能性があります。しかし、まだ石1つ分しか確認していません。

というわけで、さっきマークしたところの隣を確認してみましょう。つまり、今度は自分の石ではなくマークの方を全部1個ずらします。移動前のマークを半透明にして示しています。

ずらしたマークがまた相手の石と重なっていれば、ひっくり返せるかもしれない石が連続で置いてあるということになります。マーク用ボードに追記しましょう。今回は両端にマークはないようですが、あったら先程と同様マークを消してしまいます。

この『1つずらして重なりを確認してマークを追記する』という作業は、ひっくり返せる可能性のある石の数だけ行う必要があります。

自分の石2個で相手の石を挟むわけですから、この作業を行う回数はボードの幅-2回となります。普通のオセロは8×8なので、8-2=6回作業を繰り返す必要があります。

この作業を終えると、ひっくり返せるかもしれない石を全部マークしたボードが手に入ります。

合法手を計算する

ひっくり返せるかもしれない石を全部マークすることはできました。

そこから本当にひっくり返せる石を選別したくなるところですが、置ける場所を計算するだけならその区別は必要ありません。

肝心のその手法ですが、まずは空きマスをマークしたボードを用意します。

そして、先程入手したひっくり返せるかもしれない石ボードを1つ右にずらして重ねます。移動前のマークを半透明にして示しています。

すると、空きマスとずらしたマークが重なっている場所があります。今回の場合は右上の1マスですね。

この重なった場所が合法手、すなわち自分が石を置ける場所になります。

要するに……

この方法では、『自分の石から連続して存在する相手の石の先に空きマスが存在するかどうか』を確認しているということです。

ぶっちゃけ、何も特別なことはやっていません。全く同じアルゴリズムは、ボードを二次元配列などで用意しても実装できます。

しかし、ビットボードには演算が高速だったりメモリ使用量が少なかったりといったメリットが存在します。ビットボードの何が優れているのか、擬似コードを見ながら理解していきましょう。

擬似コードから考えるビットボードの効率性

以下に、合法手ボードを生成する擬似コードを示します。コードはこちらの記事を参考にしつつ、自分で改変しています。

ここでは上記と同様、自分(黒)の石の右のみを見るものとします。また、ボードサイズは8×8です。

シンタックスハイライトの都合が良かったのでRustのものを利用していますが、文法は正しくないのでご注意ください。

// white_board: u64 (符号なし64bit整数)
// black_board: u64 (符号なし64bit整数)

// ひっくり返せるかもしれない石のボード(最初は空っぽ)
tmp_board: u64 = 0

// 空きマスだけ1になった(ビットが立っている)ボード
blank_board: u64 = ~(white_board | black_board)

// 左右の端だけ0になっているボード(説明は後述)
side_guard: u64 = 0x7e7e7e7e7e7e7e7e

// 自分の石・マークをずらしながら計算
tmp_board = ((black_board >> 1) & white_board) & side_guard
tmp_board |= ((tmp_board >> 1) & white_board) & side_guard
tmp_board |= ((tmp_board >> 1) & white_board) & side_guard
tmp_board |= ((tmp_board >> 1) & white_board) & side_guard
tmp_board |= ((tmp_board >> 1) & white_board) & side_guard
tmp_board |= ((tmp_board >> 1) & white_board) & side_guard

// 合法手ボードを生成
legal_board: u64 = (tmp_board >> 1) & blank_board

基本的には先程の解説をなぞっているのみです。

ビット演算が分かる方はひとまずなんとなく分かるかとは思います。

ビット演算が分からない方は大まかに以下のような理解をしてください。

>>: 右シフト演算。指定した数字の数だけ全ての1を右にずらす。一番下の桁から溢れた1は消える。
- 今回の場合、石やマークを右にずらすと考えて良い。右端にたどり着いたものは本来下の行の左端にワープしてしまうが、下記のside_guardが端の石やマークを消し飛ばすのでその心配はない
&: AND演算。2つの数字を2進数として考えて、どちらの数字でも1の桁だけ1になった数字を作る。(例: 1010 & 0110 = 0010)
|: OR演算。2つの数字を2進数として考えて、どちらかの数字が1の桁だけ1になった数字を作る。(例: 1010 | 0110 = 1110)
- A |= BはA = A | Bを短く書いたもの
~: NOT演算。1つの数字を2進数として考えたときに、0と1を全て反転させる。(例: ~0010 = 1101)

補足説明: blank_board

空きマスの部分だけ1になった(ビットが立った)ボードは、以下の手順で作れます。

白の石と黒の石のORを取り、全ての石が区別なく1になっているボードを作る
1で作ったボードを反転させる

補足説明: side_guard

先に挙げた記事では「番人」とも表現されているこの数値0x7e7e7e7e7e7e7e7eは、2進数にして8×8に並べ直すと以下のようになります。

先程の説明の中で、以下のように述べました。

さて、ボードの一番右にある相手の石にもマークをつけてしまいましたが、よく考えたらこれ以上右は盤外なので、この石はひっくり返せませんね。
これは右だけでなく、ボードの端はどちらもひっくり返せないことになります。というわけで、残念ですがさっきつけたマークのうちボードの両端にあるものには消えてもらうことにしましょう。

端が0になっているこのボードとAND演算を行うことで、端にマークがあっても消滅するようになります。

メリット: メモリ効率が良い

本記事の最初で示した二次元配列を思い出してみます。

board_othello = [
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "B", "W", "W", "W", "B", "-"],
    ["-", "B", "B", "W", "B", "B", "-", "-"],
    ["-", "-", "-", "W", "B", "-", "-", "-"],
    ["-", "-", "W", "-", "B", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"],
    ["-", "-", "-", "-", "-", "-", "-", "-"]
]

1文字を8bitとした場合、この盤面は512bit=64Byteで表現されています。

一方で、ビットボードの場合は白と黒のボードがそれぞれ64bit整数なので、128bit=16Byteで表現可能です。

現代のコンピューターの性能を考えればたかが48Byte程度の差など微々たるものではありますが、オセロAIなどを作る場合は探索した盤面をいくつも覚えておく必要が生じてくるので、意外とバカにできないです。

メリット: 演算が高速

二次元配列の場合、石を探す際に64個ある配列の要素をいちいちforループで探索する必要があります。加えて、1要素ごとに条件分岐を行う必要もあります。自分の石が見つかったらそこから周囲の石も探索しなければいけません。

一方、ビットボードの場合、擬似コードを見る限りではビット演算を27回行っています。基本的に、ビット演算というのはCPUの1クロックで行えるものなので、これは明らかに高速です。8方向調べる場合でも27×8=216回の演算で済みますし、条件分岐も生じません。さらに言えば、予め相手のボードと番人ボードをAND演算したボードを用意しておけば、もう少し計算回数が減少します。

これほど演算回数を少なくできるのは、石を複数個同時に扱えているからです。コンピュータが行っているのは結局のところ簡単な数字同士の計算ですが、数字をオセロのボードに見立てることでこのような計算を可能にしています。考えた人は頭が良すぎて恐ろしいですね。

まとめ

ビットボードがなんかすごいことはなんとなく伝わったかと思います。やっていること自体は暴いてしまえばそこまで難しくはないものの、それをビット演算でいかに実現するかどうかというのは天才の所業ですね。

オセロは64bit整数でちょうど表せるので都合が良かったですが、やろうと思えば将棋なんかもビットボードにできるそうです。(まあそれはそう)

間違っていたら優しくマサカリを𝕏あたりに投げに来てください……修正しますので……